A passive component designed to resist changes in current. Inductors are often referred to as "AC resistors". The ability to resist changes in current and store energy in its magnetic field account for the bulk of the useful properties of inductors.
Current passing through an inductor will produce a magnetic field. A changing magnetic field induces a voltage which opposes the field-producing current. This property of impeding changes of current is known as inductance.
In general, the relationship between the time-varying voltage v(t) across an inductor with inductance L and the time-varying current i(t) passing through it is described by the differential equation:
v(t) = L \frac{di(t)}{dt}
When there is a sinusoidal alternating current (AC) through an inductor, a sinusoidal voltage is induced.
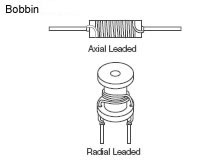
Bobbin winding inductors are for various applications, So the Bobbin is made of various materials: plastic, phenolic resin, glass, Teflon and so on.
Most bobbins are molded. Bobbin design of bobbin winding inductor usually provides terminals, pins, and/or surface mount pads to ease wire termination and to facilitate printed circuit board mounting.
Bobbin wound inductors refers to a type or method of constructin of winding inductors chokes and reactors.
An inductor constructed by placing a winding(s) on a core that has a donut shaped surface. Toroidal cores are available in many magnetic core materials within the four basic types: ferrite, powdered iron, alloy and high flux, and tape wound.
Characteristics of toroidal inductors include: self shielding (closed magnetic path), efficient energy transfer, high coupling between windings and early saturation.
"E" cores are shaped like an "E" and have a closed magnetic path like a toroidal core when configured as ungapped. The gapped "E" cores have a partially open magnetic path. The advantage of gapping an "E" core is that you can obtain higher inductance values before reaching saturation.
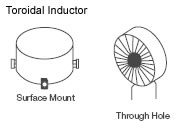
Toroidal coils are wound directly onto a toroidal core. The core may be coated or boxed to insulate it from the coil windings. In contrast, bobbin wound inductor coils are wound independently of the core. The coil must hold its shape or form until the coil is assembled onto the inductor core.
The Toroidal is a pre-formed reasonably rigid part. The Toroidal material is usually (but not always) an insulating material, hence it can provide electrical isolation between the coil and the adjoining core material provided suitable creepage distance is used.
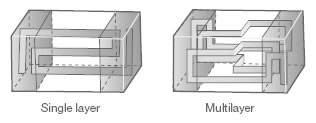
Token has developed a new family of multilayer ceramic inductors designed specifically for RF circuits in tablets and smartphones. They are characterized by their high degree of miniaturization and high Q factor.
To reach the required high Q values, Token uses new material design and process technologies as well as special dielectrics and electrode materials. A multilayer Laser Cut process offering maximum precision is also applied due to the combination of these technologies.
Ceramic is one of the common materials used for inductor cores. Its main purpose is to provide a form for the coil. In some designs it also provides the structure to hold the terminals in place.
Ceramic has a very low thermal coefficient of expansion. This allows for relatively high inductance stability over the operating temperature ranges. Ceramic has no magnetic properties. Thus, there is no increase in permeability due to the core material. Ceramic core inductors are often referred to as "air core" inductors.
Ceramic core inductors are most often used in high-frequency applications where low inductance values, very low core losses, and high Q values are required.
Ferrite is a magnetic material which consists of a mixed oxide of iron and other elements that are made to have crystalline molecular structure. The crystalline structure is created by fi ring the ferrite material at a very high temperature for a specified amount of time and profile.
The general composition of ferrites is xxFe2O4 where xx represents several metals. The most popular metal combinations are manganese and zinc (MnZn), and nickel and zinc (niZn). These metals can be easily magnetized.
Kool Mu® is a magnetic material that has an inherent distributed air gap. The distributed air gap allows the core to store higher levels of magnetic flux when compared to other magnetic materials, such as ferrites. This characteristic allows a higher DC current level to fl ow through the inductor before the inductor saturates.
Kool Mu material is an alloy that is made up of nickel and iron powder (approx. 50% of each) and is available in several permeabilities. It has a higher permeability than powdered iron and lower core losses. Kool Mu performs well in power switching applications. The relative cost is signifi cantly higher than powdered iron.
MPP is an acronym for molypermalloy powder. It is a magnetic material that has an inherent distributed air gap. The distributed air gap allows the core to store higher levels of magnetic flux when compared to other magnetic materials, such as ferrites.
This characteristic allows a higher DC current level to fl ow through the inductor before the inductor saturates. The basic raw materials are nickel, iron, and molybdenum. MPP stores higher amounts of energy and has a higher permeability than Kool Mu.
The core characteristics allow inductors to perform very well in switching power applications. Since higher energy can be stored by the core. The cost of MPP is signifi cantly higher than Kool Mu, powdered irons, and most ferrite cores with similar sizes.
Powdered iron is a magnetic material that has an inherent distributed air gap. The distributed air gap allows the core to store higher levels of magnetic flux when compared to other magnetic materials, such as ferrites.
This characteristic allows a higher DC current level to flow through the inductor before the inductor saturates. Powdered iron cores are made of nearly 100% iron. The iron particles are insulated from each other, mixed with a binder (such as phenolic or epoxy) and pressed into the fi nal core shape.
Powdered iron cores are typically the lowest cost alternative and their permeabilities typically have a more stable temperature coefficient than ferrites.
Cores constructed by stacking multiple laminations on top of each other. The laminations are offered in a variety of materials and thicknesses. Some laminations are made to have the grains oriented to minimize the core losses and give higher permeabilities. Each lamination has an insulated surface which is commonly an oxide finish. Laminated cores are used in some inductor designs but are more common in a wide variety of transformer applications.
That property of a circuit element which tends to oppose any change in the current fl owing through it.
The inductance for a given inductor is infl uenced by the core material, core shape and size, the turns count, and the shape of the coil.
Inductors most often have their inductances expressed in microhenries (μH).
The following table can be used to convert units of inductance to microhenries.
Thus, 47 mH would equal 47,000 μH.
1 henry (H) = 106 μH
1 millihenry (mH) = 103 μH
1 microhenry (μH) = 1 μH
1 nanohenry (nH) = 10-3 μH
The resistance of the inductor winding measured with no alternating current. The DCR is most often minimized in the design of an inductor. The unit of measure is ohms, and it is usually specifi ed as a maximum rating.
The DC bias current fl owing through the inductor which causes the inductance to drop by a specifi ed amount from the initial zero DC bias inductance value. Common specifi ed inductance drop percentages include 10% and 20%. It is useful to use the 10% inductance drop value for ferrite cores and 20% for powdered iron cores in energy storage applications.
The cause of the inductance to drop due to the DC bias current is related to the magnetic properties of the core. The core, and some of the space around the core, can only store a given amount of magnetic flux density. Beyond the maximum flux density point, the permeability of the core is reduced.
Thus, the inductance is caused to drop. Core saturation does not apply to "air-core" inductors. (Also see Incremental Current and Permeability)
The DC bias current flowing through the inductor which causes an inductance drop of 5% from the initial zero DC bias inductance value. This current level indicates where the inductance can be expected to drop signifi cantly if the DC bias current is increased further.
This applies mostly to ferrite cores in lieu of powdered iron. Powdered iron cores exhibit "soft" saturation characteristics. This means their inductance drop from higher DC levels is much more gradual than ferrite cores. The rate at which the inductance will drop is also a function of the core shape. (Also see Saturation Current)
The level of continuous DC current that can be passed through the inductor. This DC current level is based on a maximum temperature rise of the inductor at the maximum rated ambient temperature. The rated current is related to the inductor's ability to minimize the power losses in the winding by having a low DC resistance. It is also related to the inductor's ability to dissipate this power lost in the windings.
Thus, the rated current can be increased by reducing the DC resistance or increasing the inductor size. For low frequency current waveforms, the RMS current can be substituted for the DC rated current. The rated current is not related to the magnetic properties of the inductor. (Also see Incremental Current and Saturation Current).
In the construction of an inductor, each turn of wire or conductor acts as a capacitor plate. The combined effects of each turn can be represented as a single capacitance known as the distributed capacitance.
This capacitance is in parallel with the inductor. This parallel combination will resonate at some frequency which is called the self-resonant frequency (SRF). Lower distributed capacitances for a given inductance value will result in a higher SRF value for the inductor and vice versa. (Also see SRF)
The frequency at which the inductor's distributed capacitance resonates with the inductance. It is at this frequency that the inductance is equal to the capacitance and they cancel each other.
The inductor will act purely resistive, with a high impedance at the SRF point. The distributed capacitance is caused by the turns of wire layered on top of each other and around the core. This capacitance is in parallel to the inductance.
At frequencies above the SRF, the capacitive reactance of the parallel combination will become the dominant component. Also, the Q of the inductor is equal to zero at the SRF point since the inductive reactance is zero.
The SRF is specifi ed in MHz and is listed as a minimum value on product data sheets. (Also see Distributed Capacitance)
The Q value of an inductor is a measure of the relative losses in an inductor.
The Q is also known as the "quality factor" and is technically defi ned as the ratio of inductive reactance to effective resistance, and is represented by:
Q = \frac{XL}{Re} = \frac{2πfL}{Re}
Since XL and Re are functions of frequency, the test frequency must be given when specifying Q.
XL typically increases with frequency at a faster rate than Re at lower frequencies, and vice versa at higher frequencies.
This results is a bell-shaped curve for Q vs frequency. Re is mainly comprised of the DC resistance of the wire, the core losses and skin effect of the wire.
Based on the above formula, it can be shown that the Q is zero at the self-resonant frequency since the inductance is zero at this point.
The impedance of an inductor is the total resistance to the fl ow of current, including the AC and DC component.
The DC component of the impedance is simply the DC resistance of the winding. The AC component of the impedance includes the inductor reactance.
The following formula calculates the inductive reactance of an ideal inductor (i.e., one with no losses) to a sinusoidal AC signal:
Z = XL = 2πfL
L is in henries and f is in hertz. This equation indicates that higher impedance levels are achieved by higher inductance values or at higher frequencies.
Skin effect and core losses also add to the impedance of an inductor. (Also see Skin Effect and Core losses)
Range of ambient temperatures over which a component can be operated safely.
The operating temperature is different from the storage temperature in that it accounts for the component's self temperature rise caused by the winding loss from a given DC bias current.
This power loss is referred to as the “copper” loss and is equal to:
Power Loss = (DCR)(I2dc)
The permeability of a magnetic core is the characteristic that gives the core the ability to concentrate lines of magnetic flux. The core material, as well as the core geometry, affect the core's "effective permeability". For a given core shape, size and material, and a given winding, higher permeability magnetic materials result in higher inductance values as opposed to lower permeability materials.
The power lost by current flowing through the winding. The power loss is equal to the square of the current multiplied by the resistance of the wire (I2R). This power loss is transferred into heat.
Core losses are caused by an alternating magnetic field in the core material. The losses are a function of the operating frequency and the total magnetic flux swing. The total core losses are made up of three main components: hysteresis, eddy current and residual losses. These losses vary considerably from one magnetic material to another.
Applications such as higher power and higher frequency switching regulators and RF designs require careful core selection to yield the highest inductor performance by keeping the core losses to a minimum.
Eddy current losses are present in both the magnetic core and winding of an inductor. Eddy currents in the winding (or conductor) contribute to two main types of losses:
As for the core losses, an electric field around the flux lines in the magnetic field is generated by alternating magnetic flux. This will result in eddy currents if the magnetic core material has electrical conductivity. Losses result from this phenomenon since the eddy currents flow in a plane that is perpendicular to the magnetic flux lines.
Skin effect is the tendency for alternating current to flow near the surface of the conductor in lieu of flowing in a manner that utilizes the entire cross-sectional area of the conductor. This phenomenon causes the resistance of the conductor to increase.
The magnetic field associated with the current in the conductor causes eddy currents near the center of the conductor which opposes the flow of the main current near the center of the conductor.
The main current flow is forced further to the surface as the frequency of the alternating current increases. (Also see litz Wire)
Wire consisting of a number of separately insulated strands that are woven or bunched together such that each strand tends to take all possible positions in the cross section of the wire as a whole.
The current through each individual strand is divided equally since this wire design equalizes the flux linkages and reactance of the individual strands.
In other words, a litz conductor has lower AC losses than comparable solid-wire conductors, which becomes important as the operating frequency increases. (See also Skin Effect)
The temperature above which a ferrite core loses its magnetic properties. The core's permeability typically increases dramatically as the core temperature approaches the curie temperature, which causes the inductance to increase.
The permeability drops to near unity at the curie temperature, which causes the inductance to drop dramatically. The curie point is the temperature at which the initial permeability has dropped to 10% of its original value at room temperature.
On a given design, as inductance (turns of wire) goes up, so does the DCR.
If the permeability of the core is increased, the number of windings can be reduced, and DCR will go down.
On a given design, as inductance (turns of wire) goes up the rated current goes down.
If the permeability of the core is increased, the number of windings can be reduced and rated current will go up.
On a given design, as inductance (turns of wire) goes up, the incremental current goes down. If the permeability of the core is increased, the number of windings can be reduced and incremental current may increase or decrease.
* If the increased permeability decreases the point at which the core saturates, the actual incremental current can go down.
On a given design, as inductance (turns of wire) goes up, the distributed capacitance will also go up, and the SRF will go down.
If the permeability of the core is increased, the number of windings can be reduced, and SRF will increase (less distributed capacitance).
On a given design, as inductance (turns of wire) goes up, the Q goes down. If the permeability of the core is increased, the number of windings can be reduced and incremental current may increase or decrease (*).
A higher Q generally indicates an inductor that is a more selective filter. Inductors used in RF circuits usually have high Q's so they can be more frequency selective.
A lower Q generally indicates an attenuation over a broader range of frequencies. A ferrite bead has a low Q and is thus considered a broadband filter.
* Increased permeability can result in the Re increasing at certain frequencies resulting in a lower Q.
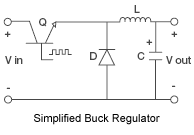
A basic dc-to-dc switching converter topology that takes an unregulated input voltage, and produces a lower, regulated output voltage. This output voltage is achieved by chopping the input voltage with a series of connected switches (transistor) that apply pulses to an averaging inductor and capacitor circuit.
A circuit or device whose purpose is to control electrical energy at a given frequency or over a range of frequencies. Groups of passive components are commonly used to construct many types of filters. These passive components include resistors, capacitors and inductors.
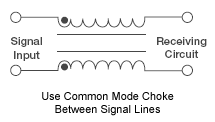
Used to attenuate common mode noise or electrical interference that is common to both electrical lines in relation to earth ground. A common mode choke is actually a transformer configured to have the common noise cancel itself in the transformer.
EMI is an acronym for electromagnetic interference. It is unwanted electrical energy in any form. EMI is often used interchangeably with "noise". Ferrite beads are the most common device used for EMI attenuation.
The condition that exists when two coupled circuits are adjusted so that the output impedance of one circuit equals the input impedance of the other circuit. There is a minimum power loss between two circuits when their connecting impedances are equal.
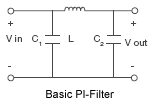
A fi lter consisting of two capacitors connected in parallel with a series inductor. These fi lters are commonly found near dc-to-dc converters to filter ripple current and voltage.
A power fi lter placed on the input to a circuit or assembly that attenuates noise introduced from the power bus. The filter is designed to reject noise within a frequency band. Typically, these filters are low-pass filters, meaning they pass low frequency signals such as the DC power, and attenuate higher frequency signals which consist mainly of noise. Band pass, or low pass filters, are commonly made up of inductor and capacitor combinations.
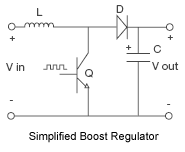
A basic dc-to-dc switching converter topology that takes an unregulated input voltage, and produces a higher, regulated output voltage. This higher output voltage is achieved by storing energy in an input inductor and then transferring the energy to the output by turning a shunt switch (transistor) on and off.
Unwanted electrical energy in a circuit that is unrelated to the desired signal. Sources of noise are most often generated by some type of switching circuit. Common sources include switching voltage regulators and clocked signals, such as digital circuits.
Download What is a Inductor? in PDF file.